Otros autores lo describen como:
Una clase muy especial de movimiento que ocurre cuando la fuerza actúa sobre un cuerpo es proporcional al desplazamiento del cuerpo desde alguna posición de equilibrio. Si esta fuerza se dirige hacia la posición de equilibrio hay un movimiento repetitivo hacia delante y hacia atrás alrededor de esta posición.
Elementos de un M.A.S
1. Oscilación: es el movimiento realizado desde cualquier posición hasta regresar de nuevo a ella, pasando por las posiciones intermedias.
2. Elongación: desplazamiento de la partícula que oscila desde la posición de equilibrio hasta cualquier posición.
3. Amplitud: es la máxima elongación, es decir, el desplazamiento máximo.
4. Período: tiempo en realizar una oscilación.
5. Frecuencia: número de oscilaciones realizadas en la unidad de tiempo (ciclo/seg=hertz).
6. Posición de equilibrio: es la posición en la cual no actúa ninguna fuerza neta sobre la partícula oscilante.

Cinemática del movimiento armónico simple
El movimiento armónico simple es un movimiento periódico de vaivén, en el que un cuerpo oscila de un lado al otro de su posición de equilibrio, en una dirección determinada, y en intervalos iguales de tiempo.
Por ejemplo, es el caso de un cuerpo colgado de un muelle oscilando arriba y abajo. El objeto oscila alrededor de la posición de equilibrio cuando se le separa de ella y se le deja en libertad. En este caso el cuerpo sube y baja.
Es también, el movimiento que realiza cada uno de los puntos de la cuerda de una guitarra cuando esta entra en vibración; pero, pongamos atención, no es el movimiento de la cuerda, sino el movimiento individual de cada uno de los puntos que podemos definir en la cuerda. El movimiento de la cuerda, un movimiento ondulatorio, es el resultado del movimiento global y simultáneo de todos los puntos de la cuerda.
Respecto a su posición de equilibrio. En un desplazamiento a lo largo del eje Ox, tomando el origen O en la posición de equilibrio, esta fuerza es tal que donde es una constante positiva y es la elongación. El signo negativo indica que en todo momento la fuerza que actúa sobre la partícula está dirigida hacía la posición de equilibrio; esto es, en dirección contraria a su elongación (la "atrae" hacia la posición de equilibrio).

Dinámica del movimiento armónico simple
El cuerpo unido a un resorte que realiza un M.A.S, forma un sistema oscilante masa-resorte. Mientras el cuerpo oscila, está sometido a una fuerza recuperadora ejercida por el resorte que obedece a la Ley de Hooke, la cual explica que: el valor de la fuerza recuperadora del resorte es proporcional a la elongación y de sentido contrario.
Mientras estiramos el resorte, la mano ejerce una fuerza de deformación sobre el resorte hacia la derecha, y el resorte ejerce una fuerza recuperadora sobre la masa hacia la izquierda.
Mientras la bola oscila pasa por estados de equilibrio en los que sobre ella actúa un F = 0 y le comunica a = 0
Al soltar la bola la fuerza recuperadora del resorte le comunica una aceleración que es proporcional a la elongación:a = - w2 x
Esta fuerza recuperadora es de tipo conservativo y el
trabajo realizado por ella se puede calcular mediante la expresión de la
energía potencial, fórmula que contiene una única variable, la elongación.
También podriamos hallar el trabajo con la formula F·x pero eso requiere
conocer el valor de F en cada momento y halla la suma de F·x a lo largo del
camino (integrar). Esto es más complicado que usar la Ep que sólo implica
conocer los valores de x iniciales y finales y multiplicar por w2.
Curva de energía potencial
La función Ep=mω2x2/2
representa una parábola cuyo vértice está en el origen, que tiene un mínimo en x=0 cuyo valor es Ep=0.
Las región donde se puede mover
la partícula está determinada por la condición de que la energía cinética ha de
ser mayor o igual a cero Ek>=0.
En otras palabras, que la energía total sea mayor o igual que la energía
potencial E>=Ep.
Si la partícula tiene una energía total E,
la partícula solamente se podrá mover en la región comprendida entre-A y +A,
siendo A la amplitud de su M.A.S.
El módulo y el sentido de la
fuerza vienen dados por la pendiente de la recta tangente cambiada de signo.
Por tanto, la fuerza que actúa sobre la partícula es negativa a la derecha del
origen y positiva a la izquierda.
En el origen la pendiente es
nula, la fuerza es nula, una situación de equilibrio, que por coincidir con un
mínimo de la energía potencial es de carácter estable.
Energía del movimiento armónico simple
Las fuerzas involucradas en un movimiento armónico simple son centrales y, por tanto, conservativas. En consecuencia, se puede definir un campo escalar llamado energía potencial (Ep) asociado a la fuerza. Para hallar la expresión de la energía potencial, basta con integrar la expresión de la fuerza (esto es extensible a todas las fuerzas conservativas) y cambiarla de signo, obteniéndose:
La energía potencial alcanza su máximo en los extremos de la trayectoria y tiene valor nulo (cero) en el punto x = 0, es decir el punto de equilibrio.
La energía cinética cambiará a lo largo de las oscilaciones pues lo hace la velocidad:
La energía cinética es nula en -A o +A (v=0) y el valor máximo se alcanza en el punto de equilibrio (máxima velocidad Aω).
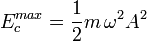
Como sólo actúan fuerzas conservativas, la energía mecánica (suma de la energía cinética y potencial) permanece constante.

Finalmente, al ser la energía mecánica constante, puede calcularse fácilmente considerando los casos en los que la velocidad de la partícula es nula y por lo tanto la energía potencial es máxima, es decir, en los puntos x = -A y x = A. Se obtiene entonces que,
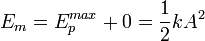
O también cuando la velocidad de la partícula es máxima y la energía potencial nula, en el punto de equilibrio 

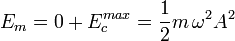







No hay comentarios:
Publicar un comentario